


Next: Image Restoration
Up: Image Manipulations
Previous: Background Estimates
Transformations
Depending on the further reductions the data may be transformed into
the coordinate system which is most relevant for the physical
interpretation. This will typically be used when certain
characteristics of the data will appear as a linear relation in the
new coordinates. These transformations involve non-linear rebinning
as discussed in Section 2.2.3. To conserve flux in the new
system, the pixel values must be corrected by the Jacobian determinant
 in Equation 2.15.
in Equation 2.15.
For spectra a transformation from wavelength to frequency is used to
identify spectral regions which follow a power law. This
transformation is given by
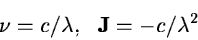 |
(2.21) |
where 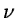 is the frequency and
is the frequency and 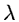 is wavelength.
The intensities I are translated to a logarithmic scale (e.g. magnitudes
is wavelength.
The intensities I are translated to a logarithmic scale (e.g. magnitudes
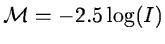 )
so that a power law spectrum appears linear.
)
so that a power law spectrum appears linear.
In the classification of galaxies, ellipticals can be distinguished on
their radial surface brightness profile which can be approximated
by
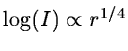 .
This gives the transformation formula
.
This gives the transformation formula
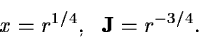 |
(2.22) |
Since the intensity profile only should be resampled, the flux
correction is not applied in this case. A logarithmic scale is also
used here to achieve a linear relation. An example is given in
Figure 2.9.
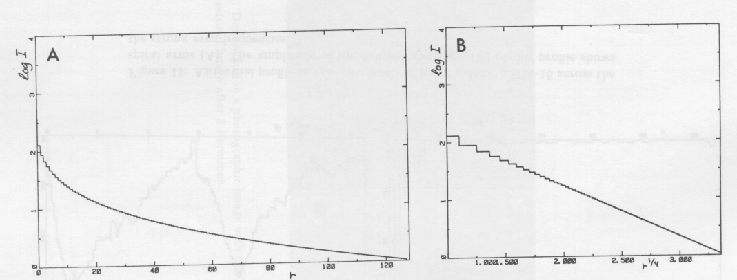
Figure 2.9:
The radial profile of an elliptical galaxy shown with linear
steps (A) and rebinned to r1/4 increments (B).
 |
Whereas the transforms mentioned above only perform a non-linear
rebinning of the data, the Fourier transform converts a spatial image
into the frequency domain. This transform has two main applications
namely analysis of periodic phenomena and convolution due to its
special properties. The transform can be given as
![\begin{displaymath}{\cal F} (u,v) =
\frac{1}{N} \sum_{j=0}^{N-1} \sum_{k=0}^{N-1} F(j,k)
\exp \left[ \frac{-2\pi i}{N} (uj + vk) \right]
\end{displaymath}](img101.gif) |
(2.23) |
where (u,v) are the spatial frequencies and i denotes the imaginary part.
The corresponding inverse transform is then
![\begin{displaymath}F (j,k) =
\frac{1}{N} \sum_{j=0}^{N-1} \sum_{k=0}^{N-1} {\cal F} (u,v)
\exp \left[ \frac{2\pi i}{N} (uj + vk) \right] .
\end{displaymath}](img102.gif) |
(2.24) |
Special numeric techniques, called Fast Fourier Transforms or FFT, can
significantly decrease the time needed to compute these transforms.
They are optimized for images with a size equal to a power of 2 (see
e.g. Hunt 1969) but can also be used in other cases.
To analysis the periodic occurrence of features in time series,
spectra, or images the amplitude of the Fourier transform or the power
spectrum is used. The power spectrum 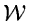 of the function F is
given by
of the function F is
given by
 |
(2.25) |
Peaks in  indicate the presence of specific frequencies while
the continuum originates from a combination of objects and noise.
Since the Fourier transform assumes the image to occur periodically,
discontinuities at the edges of the image will produce artificial
contributions to the power spectrum. Thus, care should be taken to
remove systematic background variations to avoid this happening. As
an example of using Fourier transforms to extract information from a
frame, an azimuthal intensity profile of the spiral galaxy A0526-16
is shown in Figure 2.10.
indicate the presence of specific frequencies while
the continuum originates from a combination of objects and noise.
Since the Fourier transform assumes the image to occur periodically,
discontinuities at the edges of the image will produce artificial
contributions to the power spectrum. Thus, care should be taken to
remove systematic background variations to avoid this happening. As
an example of using Fourier transforms to extract information from a
frame, an azimuthal intensity profile of the spiral galaxy A0526-16
is shown in Figure 2.10.
Figure 2.10:
Azimuthal profile in the inner parts of a spiral galaxy A0526-16
across the spiral arms (A). The amplitude of the Fourier
transform (B) of this profile shows the strong even frequencies.
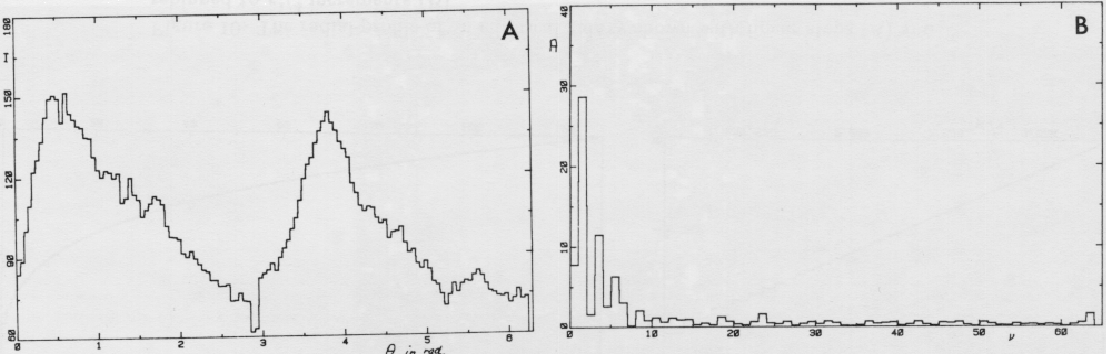 |
The radius was chosen so that the profile intersects the spiral
pattern in the inner parts of the galaxy. In the amplitude plot of
the Fourier transform, it can be seen that the spiral pattern mainly
contains even frequency components. The 4th and 6thharmonic indicates that the wave is asymmetric due to non-linear
effects in the spiral density wave.
It is possible to use the transformation for convolutions because this
operation corresponds to a multiplication in the frequency domain :
![\begin{displaymath}{\cal O_F} [ F(j,k) \otimes H(j,k) ] = {\cal F}(u,v)\,{\cal H}(u,v)
\end{displaymath}](img107.gif) |
(2.26) |
where 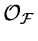 and
and 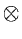 denote the Fourier transform
and convolution operators, respectively.
Especially when the convolution matrix is large it is more efficient to
perform the operation in frequency than in spatial domain.
denote the Fourier transform
and convolution operators, respectively.
Especially when the convolution matrix is large it is more efficient to
perform the operation in frequency than in spatial domain.



Next: Image Restoration
Up: Image Manipulations
Previous: Background Estimates
Petra Nass
1999-06-15
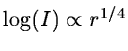 .
This gives the transformation formula
.
This gives the transformation formula

![]() of the function F is
given by
of the function F is
given by
