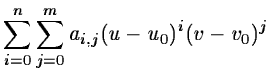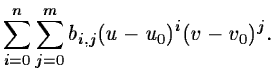


Next: Image Manipulations
Up: Raw to Calibrated Data
Previous: Response Calibration
Geometric Corrections
Most imaging systems contain intrinsic geometric distortions.
Although they can often be disregarded for small field corrections
they must be applied when image tubes or dispersive elements (e.g. in
spectrographs) are used. The actual form of the distortions is
determined by observing a known grid of points or spectral lines.
Normally, a power series is fitted to the point giving the coordinate
transformation
| x = X(u,v) |
= |
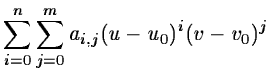 |
(2.13) |
| y = Y(u,v) |
= |
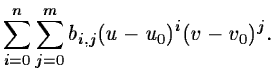 |
(2.14) |
where (u0,u0) is an arbitrary reference point. The area of a
pixel is changed by this transformation with an amount
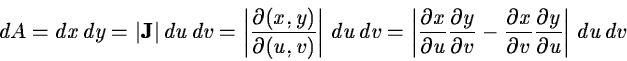 |
(2.15) |
where 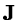 is the Jacobian determinant. The intensity values in
the transformed frame must be corrected by this function so that the
flux is maintained both locally and globally. A wavelength
transformation for an image tube spectrum is shown in
Figure 2.5 where both resulting spectra with and
without flux correction are given.
is the Jacobian determinant. The intensity values in
the transformed frame must be corrected by this function so that the
flux is maintained both locally and globally. A wavelength
transformation for an image tube spectrum is shown in
Figure 2.5 where both resulting spectra with and
without flux correction are given.
Figure 2.5:
A dispersion curve (A) for an IDS spectrum with the linear
term omitted. The spectrum rebinned to wavelength is shown
with (B1) and without the Jacobian determinant correction (B2).
 |
Although this is mathematically very simple, it gives significant
numeric problems due to the finite size of pixels. The main problem
is that one has to assume a certain distribution of flux inside a
pixel e.g. constant. This assumption may affect the detailed local
flux conservation and introduce high frequence error in the result. A
further problem is the potential change of the noise distribution due
to the interpolation scheme used. This can be solved be careful
assignment of weight factors or by simply reducing the high frequence
noise in the original frame by smoothing.



Next: Image Manipulations
Up: Raw to Calibrated Data
Previous: Response Calibration
Petra Nass
1999-06-15