 , corresponding to the observation of an
object
, corresponding to the observation of an
object 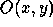 through an optical system. If the
imaging system is linear and shift-invariant, the relation between
the object and the image in the same coordinate frame is a
convolution:
through an optical system. If the
imaging system is linear and shift-invariant, the relation between
the object and the image in the same coordinate frame is a
convolution:
Consider an image characterized by its intensity
distribution  , corresponding to the observation of an
object
, corresponding to the observation of an
object 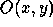 through an optical system. If the
imaging system is linear and shift-invariant, the relation between
the object and the image in the same coordinate frame is a
convolution:
through an optical system. If the
imaging system is linear and shift-invariant, the relation between
the object and the image in the same coordinate frame is a
convolution:
 is the point spread function (PSF) of the imaging system, and
is the point spread function (PSF) of the imaging system, and
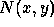 is an additive noise. In Fourier space we have:
is an additive noise. In Fourier space we have:

We want to determine  knowing
knowing  and
and  . This
inverse problem has led to a large amount of work, the main difficulties
being the existence of: (i) a cut-off frequency of the
PSF, and (ii) an intensity noise (see for example [6]).
. This
inverse problem has led to a large amount of work, the main difficulties
being the existence of: (i) a cut-off frequency of the
PSF, and (ii) an intensity noise (see for example [6]).
Equation ![]() is always an ill-posed problem.
This means that there is not a unique least-squares solution of minimal norm
is always an ill-posed problem.
This means that there is not a unique least-squares solution of minimal norm
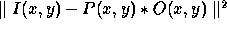 and a regularization is
necessary.
and a regularization is
necessary.
The best restoration algorithms are generally iterative [24]. Van Cittert [41] proposed the following iteration:
where 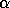 is a converging parameter generally taken as 1. In
this equation, the object distribution is modified by adding a term
proportional to the residual. But this algorithm diverges when we
have noise [12]. Another iterative algorithm is provided by
the minimization of the norm
is a converging parameter generally taken as 1. In
this equation, the object distribution is modified by adding a term
proportional to the residual. But this algorithm diverges when we
have noise [12]. Another iterative algorithm is provided by
the minimization of the norm 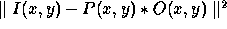 [21] and leads to:
[21] and leads to:
where 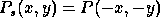 .
.
Tikhonov's regularization [40] consists of minimizing the term:

where H corresponds to a high-pass filter.
This criterion contains two terms;
the first one,  , expresses
fidelity to the data
, expresses
fidelity to the data 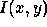 and the second one,
and the second one, 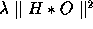 , smoothness of the restored image.
, smoothness of the restored image.  is the
regularization parameter and represents the trade-off between
fidelity to the data and the restored image smoothness. Finding
the optimal value
is the
regularization parameter and represents the trade-off between
fidelity to the data and the restored image smoothness. Finding
the optimal value 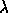 necessitates use of numeric techniques such as
Cross-Validation [15] [14].
necessitates use of numeric techniques such as
Cross-Validation [15] [14].
This method works well, but it is relatively long and produces smoothed images. This second point can be a real problem when we seek compact structures as is the case in astronomical imaging.
An iterative approach for computing maximum likelihood estimates may be used. The Lucy method [,,] uses such an iterative approach:
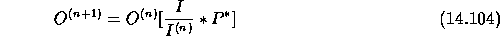
and

where 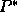 is the conjugate of the PSF.
is the conjugate of the PSF.