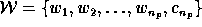 is:
is:
If the wavelet is the difference between two resolutions,
an evident reconstruction for a wavelet transform
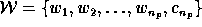 is:
is:
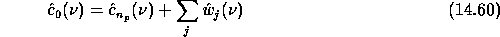
But this is a particular case and other wavelet functions can be chosen. The reconstruction can be done step by step, starting from the lowest resolution. At each scale, we have the relations:

we look for 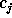 knowing
knowing  ,
,  , h and g.
We restore
, h and g.
We restore  with a least mean square estimator:
with a least mean square estimator:
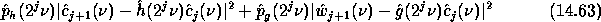
is minimum. 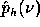 and
and 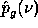 are weight
functions which permit a general solution to the
restoration of
are weight
functions which permit a general solution to the
restoration of 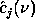 . By
. By 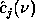 derivation we get:
derivation we get:
where the conjugate filters have the expression:
It is easy to see that these filters satisfy the exact reconstruction
equation ![]() . In fact, equations
. In fact, equations
![]() and
and ![]() give the
general solution to this equation. In this analysis, the
Shannon sampling condition is always respected. No aliasing
exists, so that the dealiasing condition
give the
general solution to this equation. In this analysis, the
Shannon sampling condition is always respected. No aliasing
exists, so that the dealiasing condition ![]() is not
necessary.
is not
necessary.
The denominator is reduced if we choose:
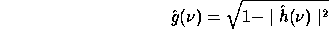
This corresponds to the case where the wavelet is the difference between the square of two resolutions:
: Left, the interpolation function 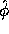 and right, the wavelet
and right, the wavelet 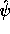 .
.
: On left, the filter  , and on right the filter
, and on right the filter 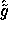 .
.
We plot in figure ![]() the chosen scaling function
derived from a B-spline of degree
3 in the frequency space and
its resulting wavelet function. Their
conjugate functions are plotted in figure
the chosen scaling function
derived from a B-spline of degree
3 in the frequency space and
its resulting wavelet function. Their
conjugate functions are plotted in figure ![]() .
.
The reconstruction algorithm is:
 . We iterate:
. We iterate:
 by
by  .
.
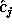 by
by
 .
.
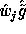 and
and 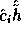 gives the
image
gives the
image 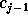 .
.
The use of a scaling function with a cut-off frequency allows a reduction of sampling at each scale, and limits the computing time and the memory size.