The Laplacian Pyramid has been developed by Burt and Adelson in 1981 [4] in order to compress images. After the filtering, only one sample out of two is kept. The number of pixels decreases by a factor two at each scale.
The convolution is done with the filter h by keeping one sample out
of two (see figure ![]() ):
):

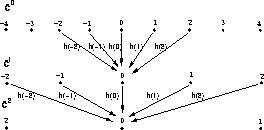
Figure: Passage from 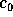 to
to 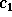 , and from
, and from 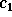 to
to 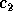 .
.
To reconstruct 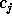 from
from 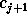 , we need to calculate the difference
signal
, we need to calculate the difference
signal 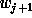 .
.

where 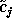 is the signal reconstructed by the following operation
(see figure
is the signal reconstructed by the following operation
(see figure ![]() ):
):

In two dimensions, the method is similar. The convolution is done by keeping one sample out of two in the two directions. We have:
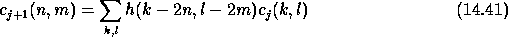
and 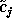 is:
is:
The number of samples is divided by four. If the image size is  ,
then the pyramid size is
,
then the pyramid size is 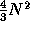 . We get a pyramidal structure
(see figure
. We get a pyramidal structure
(see figure ![]() ).
).
The laplacian pyramid leads to an analysis with four wavelets [3] and there is no invariance to translation.