 are the scalar products at pixels k of the function
are the scalar products at pixels k of the function
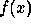 with a scaling function
with a scaling function  which corresponds to a low
pass filter.
which corresponds to a low
pass filter.
The discrete approach of the wavelet transform can be done with the
special version of the so-called à trous algorithm (with
holes) [,]. One assumes that the sampled data
 are the scalar products at pixels k of the function
are the scalar products at pixels k of the function
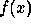 with a scaling function
with a scaling function  which corresponds to a low
pass filter.
which corresponds to a low
pass filter.
The first filtering is then performed by a twice magnified scale
leading to the 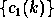 set. The signal difference
set. The signal difference 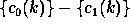 contains the information between these two scales and is
the discrete set associated with the wavelet transform corresponding
to
contains the information between these two scales and is
the discrete set associated with the wavelet transform corresponding
to 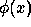 . The associated wavelet is therefore
. The associated wavelet is therefore  .
.

The distance between samples increasing by a factor
2 from the scale 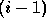 ( i > 0 ) to the next one,
( i > 0 ) to the next one,  is given by:
is given by:
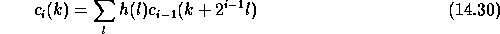
and the discrete wavelet transform 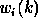 by:
by:

The coefficients 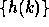 derive from the scaling function
derive from the scaling function 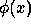 :
:

The algorithm allowing one to rebuild the data frame is evident: the
last smoothed array 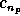 is added to all the differences
is added to all the differences 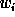 .
.
If we choose the linear interpolation for the scaling function 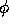 (see figure
(see figure ![]() ):
):

we have:
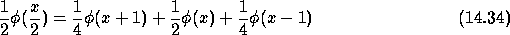
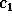 is obtained by:
is obtained by:

and  is obtained from
is obtained from 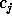 by:
by:
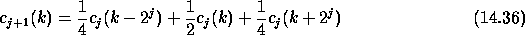
The figure ![]() shows the wavelet
associated to the scaling function.
shows the wavelet
associated to the scaling function.
The wavelet coefficients at the scale j are:
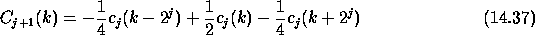
The above à trous algorithm is easily extensible to the two
dimensional space. This leads to a convolution with a mask of 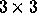 pixels for the wavelet connected to linear interpolation. The coefficents
of the mask are:
pixels for the wavelet connected to linear interpolation. The coefficents
of the mask are:

At each scale j, we obtain a set 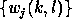 (we will call it
wavelet plane in the following), which has the same number of pixels
as the image.
(we will call it
wavelet plane in the following), which has the same number of pixels
as the image.
If we choose a  -spline for the scaling function, the coefficients
of the convolution mask in one dimension are
(
-spline for the scaling function, the coefficients
of the convolution mask in one dimension are
( ), and
in two dimensions:
), and
in two dimensions:
