


Next: Discussion
Up: CCD Detectors
Previous: CCD Detectors
Introduction
The nominal output Xij of a CCD-element to a quantum of light Iijcan be given as
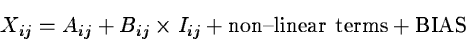 |
(18.1) |
This equation does not account for charge transfer inefficiencies and other
effects known to exist in CCDs.
The dark current and the cold columns contribute to the additive term A; the
quantum- and transfer-efficiency enter into the multiplicative term
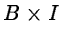 .
It is known that the response of the CCD is essentially linear so
the non-linear terms are generally neglected. The Bias is normally added to the
output electronically to avoid problems with digitising values near to zero.
.
It is known that the response of the CCD is essentially linear so
the non-linear terms are generally neglected. The Bias is normally added to the
output electronically to avoid problems with digitising values near to zero.
The objective of the first step in reducing CCD-images is to determine the
relative intensity Iij of a science data frame. In order to do this,
two more frames are required in addition to the science picture, namely:
- FLAT-frames to determine the term Bij, and
- DARK-frames to describe the term Aij.
FLAT-fields are made by illuminating the CCD with a uniformly emitting
source. The Flat-field then describes the sensitivity over the CCD which is
not uniform. For FLAT-field exposures and SCIENCE-frames we get from
Equation (B.1)
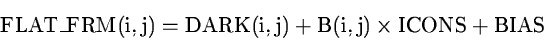 |
(18.2) |
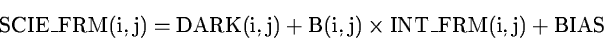 |
(18.3) |
where ICONS represents a flux from a uniform source, and BIAS is a constant
signal which is added to the video signal of the CCD before being digitised.
The DARK-current is measured in the absence of any external input signal:
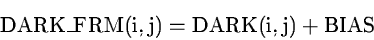 |
(18.4) |
Combining Eqs.(B.2), (B.3) and
(B.4) we isolate:
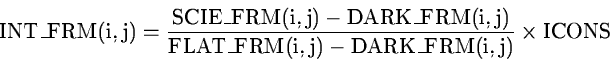 |
(18.5) |
ICONS can be any number. If set to the average signal of the dark-corrected
FLAT-frame or a subimage thereof:
 |
(18.6) |
then the reduced intensity frame INT_FRM will have similar data values as
the original SCIE_FRM.



Next: Discussion
Up: CCD Detectors
Previous: CCD Detectors
Petra Nass
1999-06-15
![]() .
It is known that the response of the CCD is essentially linear so
the non-linear terms are generally neglected. The Bias is normally added to the
output electronically to avoid problems with digitising values near to zero.
.
It is known that the response of the CCD is essentially linear so
the non-linear terms are generally neglected. The Bias is normally added to the
output electronically to avoid problems with digitising values near to zero.