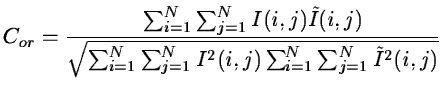 |
(14.95) |
 gives a
classical criterion. The correlation coefficient is:
gives a
classical criterion. The correlation coefficient is:
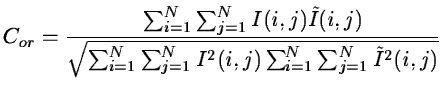 |
(14.95) |
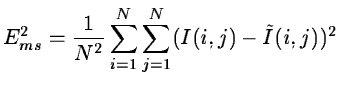 |
(14.96) |
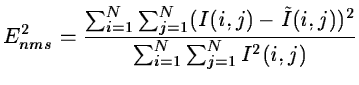 |
(14.97) |
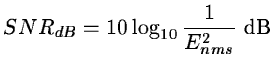 |
(14.98) |
These criteria are not sufficient, they give no information on the resulting resolution. A complete criterion must take into account the resolution. For each dyadic scale, we can compute the correlation coefficient and the quadratic error between the wavelet transforms of the original and the restored images. Hence, we can compare, the quality of the restoration for each resolution.
Figures 14.21 and 14.22 show the comparison of three images with a reference image. Data20 is a simulated noisy image, median and wave are the output images after respectively applying a median filter, and a thresholding in the wavelet space. These curves show that the thresholding in the wavelet space is better than the median at all the scales.