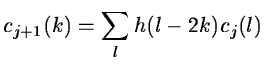 |
(14.38) |
The convolution is done with the filter h by keeping one sample out
of two (see figure 14.7):
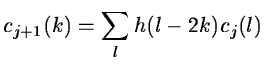 |
(14.38) |
To reconstruct cj from cj+1, we need to calculate the difference
signal wj+1.
| (14.39) |
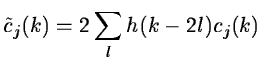 |
(14.40) |
In two dimensions, the method is similar. The convolution is done
by keeping one sample out of two in the two directions. We have:
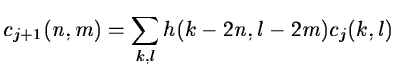 |
(14.41) |
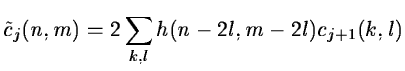 |
(14.42) |
The number of samples is divided by four. If the image size is ![]() ,
then the pyramid size is
,
then the pyramid size is
![]() .
We get a pyramidal structure
(see figure 14.9).
.
We get a pyramidal structure
(see figure 14.9).
The laplacian pyramid leads to an analysis with four wavelets [3] and there is no invariance to translation.