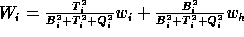


Next: Adaptive filtering from
Up: Noise reduction from
Previous: The Wiener-like filtering
In the above process, we do not use the information between the wavelet
coefficients at different scales. We modify the previous
algorithm by introducing a prediction 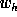 of the wavelet coefficient from
the upper scale. This prediction could be determined from the regression
[2] between the two scales but better results are obtained
when we only set
of the wavelet coefficient from
the upper scale. This prediction could be determined from the regression
[2] between the two scales but better results are obtained
when we only set 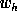 to
to 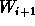 . Between the expectation
coefficient
. Between the expectation
coefficient 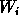 and the prediction, a dispersion exists where we
assume that it is a Gaussian distribution:
and the prediction, a dispersion exists where we
assume that it is a Gaussian distribution:
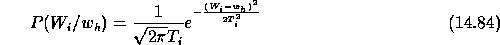
The relation which gives the coefficient 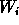 knowing
knowing 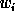 and
and 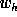 is:
is:
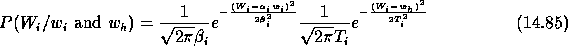
with:

and:

This follows a Gaussian distribution with a mathematical expectation:
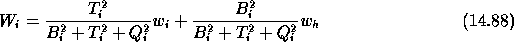
with:

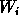 is the barycentre of the three values
is the barycentre of the three values 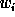 ,
, 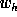 , 0 with the
weights
, 0 with the
weights 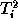 ,
, 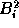 ,
, 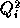 . The particular cases are:
. The particular cases are:
- If the noise is large (
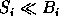 ) and even if the correlation
between the two scales is good (
) and even if the correlation
between the two scales is good (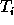 is low), we get
is low), we get 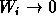 .
.
- if
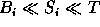 then
then 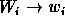 .
.
- if
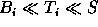 then
then 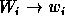 .
.
- if
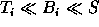 then
then 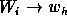 .
.
At each scale, by changing all the wavelet coefficients 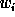 of the
plane by the estimate value
of the
plane by the estimate value 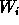 , we get a Hierarchical Wiener
Filter. The algorithm is:
, we get a Hierarchical Wiener
Filter. The algorithm is:
- Compute the wavelet transform of the data. We get
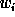 .
.
- Estimate the standard deviation of the noise
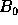 of the first plane
from the histogram of
of the first plane
from the histogram of 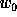 .
.
- Set i to the index associated with the last plane: i = n
- Estimate the standard deviation of the noise
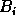 from
from 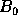 .
.
-
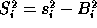 where
where 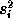 is the variance of
is the variance of 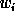
- Set
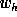 to
to 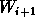 and compute the standard deviation
and compute the standard deviation 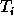 of
of  .
.
-
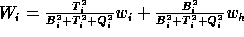
- i = i - 1. If i > 0 go to 4
- Reconstruct the picture
Rein Warmels
Mon Jan 22 15:08:15 MET 1996
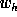 of the wavelet coefficient from
the upper scale. This prediction could be determined from the regression
[2] between the two scales but better results are obtained
when we only set
of the wavelet coefficient from
the upper scale. This prediction could be determined from the regression
[2] between the two scales but better results are obtained
when we only set 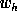 to
to 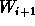 . Between the expectation
coefficient
. Between the expectation
coefficient 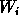 and the prediction, a dispersion exists where we
assume that it is a Gaussian distribution:
and the prediction, a dispersion exists where we
assume that it is a Gaussian distribution:
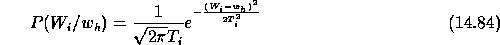
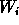 knowing
knowing 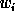 and
and 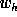 is:
is:
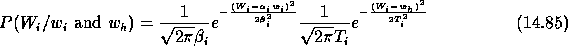


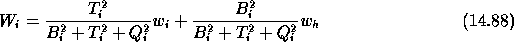

 is the barycentre of the three values
is the barycentre of the three values 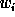 ,
, 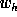 , 0 with the
weights
, 0 with the
weights 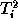 ,
, 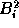 ,
, 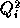 . The particular cases are:
. The particular cases are:
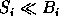 ) and even if the correlation
between the two scales is good (
) and even if the correlation
between the two scales is good (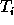 is low), we get
is low), we get 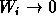 .
.
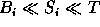 then
then 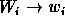 .
.
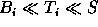 then
then 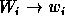 .
.
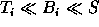 then
then 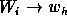 .
.
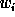 of the
plane by the estimate value
of the
plane by the estimate value 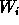 , we get a Hierarchical Wiener
Filter. The algorithm is:
, we get a Hierarchical Wiener
Filter. The algorithm is:
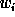 .
.
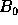 of the first plane
from the histogram of
of the first plane
from the histogram of 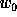 .
.
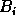 from
from 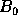 .
.
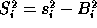 where
where 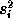 is the variance of
is the variance of 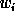
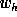 to
to 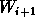 and compute the standard deviation
and compute the standard deviation 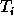 of
of  .
.