


Next: Test statistics
Up: Basic principles of
Previous: Signals and their
Paradoxically, signal detection is concerned with fitting models to
supposedly random series similarly to mathematical proofs by
reductio ad absurdum of the antithesis. That is, the hypothesis
(antithesis) 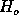 is made, that the observed series
is made, that the observed series 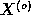 has
properties of a pure noise series,
has
properties of a pure noise series, 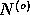 . Then, a model is fitted
and series
. Then, a model is fitted
and series 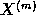 and
and 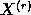 are obtained. If the quality of the
model fits to the observations
are obtained. If the quality of the
model fits to the observations 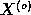 does not significantly differ
from the quality of a fit to pure noise
does not significantly differ
from the quality of a fit to pure noise 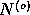 , then
, then 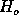 is true
and we say that
is true
and we say that 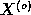 contains no signal but noise. In the
opposite case of model fitting
contains no signal but noise. In the
opposite case of model fitting 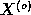 significantly better than
significantly better than
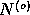 , we reject
, we reject 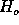 and say that the model signal was detected
in
and say that the model signal was detected
in 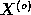 . The difference is significant (at some level) if it is
not likely (at this level) to occur between two different realizations
of the noise
. The difference is significant (at some level) if it is
not likely (at this level) to occur between two different realizations
of the noise 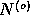 .
.
The quality of the fit is evaluated using a function S of the series
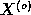 ,
, 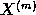 , and
, and 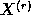 . A function of random variables,
such as
. A function of random variables,
such as 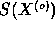 , is a random variable itself and is called a
statistic. A random variable S is characterized by its probability
distribution function. Following
, is a random variable itself and is called a
statistic. A random variable S is characterized by its probability
distribution function. Following 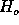 we use the distribution of S
for pure noise signal
we use the distribution of S
for pure noise signal 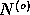 ,
, 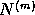 and
and 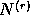 , to be
denoted
, to be
denoted 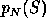 or simply
or simply 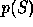 . Precisely, we shall use the
cumulative probability distribution function which for a given
critical value of the statistic
. Precisely, we shall use the
cumulative probability distribution function which for a given
critical value of the statistic 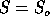 supplies the probability
supplies the probability
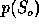 for the observed S to fall on one side of the
for the observed S to fall on one side of the 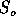 .
.
The observed value of the statistic and its probability distribution,
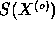 and
and 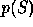 respectively, are used to obtain the
probability
respectively, are used to obtain the
probability 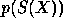 of
of 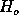 being true. That is, if p turns out
small,
being true. That is, if p turns out
small,  ,
, 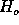 is improbable and
is improbable and 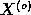 has no properties
of
has no properties
of 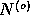 . Then we say that the model signal has been detected at
the confidence level
. Then we say that the model signal has been detected at
the confidence level 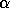 . The smaller
. The smaller 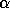 is, the more
convincing (significant) is the detection. The special realization of
a random series which consists of independent variables of common
(gaussian) distribution is called (gaussian) white noise. We assume
here that the noise
is, the more
convincing (significant) is the detection. The special realization of
a random series which consists of independent variables of common
(gaussian) distribution is called (gaussian) white noise. We assume
here that the noise 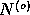 is white noise. Note that in the signal
detection process, frequency
is white noise. Note that in the signal
detection process, frequency  and lag l are considered
independent variables and do not count as parameters.
and lag l are considered
independent variables and do not count as parameters.
Summarizing, the basis for the determination of the properties of a an
observed time series is a test statistic, S, with known probability
distribution for (white) noise, 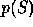 .
.
Let 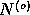 consist of
consist of 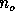 random variables and let a given model
have
random variables and let a given model
have 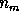 parameters. Then the modeled series
parameters. Then the modeled series 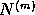 corresponds
to a combination of
corresponds
to a combination of 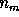 random variables and the residual series
random variables and the residual series
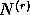 corresponds to a combination of
corresponds to a combination of 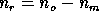 random
variables. The proof rests on the observation that orthogonal
transformations convert vectors of independent variables into vectors
of independent variables. Let us consider an approximately linear
model with matrix
random
variables. The proof rests on the observation that orthogonal
transformations convert vectors of independent variables into vectors
of independent variables. Let us consider an approximately linear
model with matrix 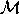 so that
so that 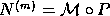 ,
where P is a vector of
,
where P is a vector of 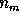 parameters. Then
parameters. Then 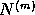 spans a
vector space with no more than
spans a
vector space with no more than 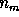 orthogonal vectors (dimensions).
The numbers
orthogonal vectors (dimensions).
The numbers 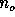 ,
, 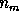 and
and 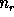 are called the numbers of degrees
of freedom of the observations, the model fit, and the residuals,
respectively.
are called the numbers of degrees
of freedom of the observations, the model fit, and the residuals,
respectively.



Next: Test statistics
Up: Basic principles of
Previous: Signals and their
Rein Warmels
Mon Jan 22 15:08:15 MET 1996
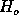 is made, that the observed series
is made, that the observed series 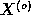 has
properties of a pure noise series,
has
properties of a pure noise series, 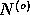 . Then, a model is fitted
and series
. Then, a model is fitted
and series 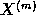 and
and 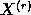 are obtained. If the quality of the
model fits to the observations
are obtained. If the quality of the
model fits to the observations 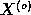 does not significantly differ
from the quality of a fit to pure noise
does not significantly differ
from the quality of a fit to pure noise 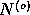 , then
, then 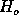 is true
and we say that
is true
and we say that 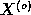 contains no signal but noise. In the
opposite case of model fitting
contains no signal but noise. In the
opposite case of model fitting 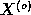 significantly better than
significantly better than
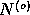 , we reject
, we reject 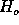 and say that the model signal was detected
in
and say that the model signal was detected
in 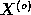 . The difference is significant (at some level) if it is
not likely (at this level) to occur between two different realizations
of the noise
. The difference is significant (at some level) if it is
not likely (at this level) to occur between two different realizations
of the noise 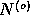 .
.
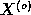 ,
, 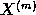 , and
, and 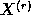 . A function of random variables,
such as
. A function of random variables,
such as 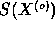 , is a random variable itself and is called a
statistic. A random variable S is characterized by its probability
distribution function. Following
, is a random variable itself and is called a
statistic. A random variable S is characterized by its probability
distribution function. Following 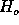 we use the distribution of S
for pure noise signal
we use the distribution of S
for pure noise signal 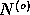 ,
, 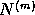 and
and 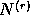 , to be
denoted
, to be
denoted 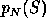 or simply
or simply 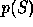 . Precisely, we shall use the
cumulative probability distribution function which for a given
critical value of the statistic
. Precisely, we shall use the
cumulative probability distribution function which for a given
critical value of the statistic 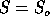 supplies the probability
supplies the probability
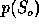 for the observed S to fall on one side of the
for the observed S to fall on one side of the 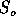 .
.
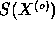 and
and 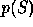 respectively, are used to obtain the
probability
respectively, are used to obtain the
probability 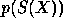 of
of 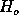 being true. That is, if p turns out
small,
being true. That is, if p turns out
small,  ,
, 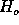 is improbable and
is improbable and 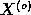 has no properties
of
has no properties
of 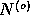 . Then we say that the model signal has been detected at
the confidence level
. Then we say that the model signal has been detected at
the confidence level 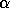 . The smaller
. The smaller 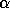 is, the more
convincing (significant) is the detection. The special realization of
a random series which consists of independent variables of common
(gaussian) distribution is called (gaussian) white noise. We assume
here that the noise
is, the more
convincing (significant) is the detection. The special realization of
a random series which consists of independent variables of common
(gaussian) distribution is called (gaussian) white noise. We assume
here that the noise 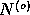 is white noise. Note that in the signal
detection process, frequency
is white noise. Note that in the signal
detection process, frequency  and lag l are considered
independent variables and do not count as parameters.
and lag l are considered
independent variables and do not count as parameters.
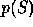 .
.
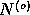 consist of
consist of 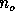 random variables and let a given model
have
random variables and let a given model
have 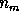 parameters. Then the modeled series
parameters. Then the modeled series 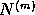 corresponds
to a combination of
corresponds
to a combination of 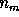 random variables and the residual series
random variables and the residual series
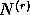 corresponds to a combination of
corresponds to a combination of 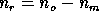 random
variables. The proof rests on the observation that orthogonal
transformations convert vectors of independent variables into vectors
of independent variables. Let us consider an approximately linear
model with matrix
random
variables. The proof rests on the observation that orthogonal
transformations convert vectors of independent variables into vectors
of independent variables. Let us consider an approximately linear
model with matrix 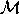 so that
so that 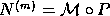 ,
where P is a vector of
,
where P is a vector of 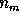 parameters. Then
parameters. Then 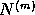 spans a
vector space with no more than
spans a
vector space with no more than 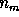 orthogonal vectors (dimensions).
The numbers
orthogonal vectors (dimensions).
The numbers 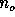 ,
, 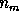 and
and 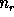 are called the numbers of degrees
of freedom of the observations, the model fit, and the residuals,
respectively.
are called the numbers of degrees
of freedom of the observations, the model fit, and the residuals,
respectively.