The Echelle Relation

The wavelength calibration involves a physical equation, the echelle relation and regression analysis to achieve estimates of the dispersion relation. Provided that the echelle dispersion is performed with a grating, any echelle spectrum can be calibrated usually with four lines used as pre-identifications and a catalog of laboratory wavelengths associated to the calibration lamp. The achieved accuracy is usually in the range 0.2 - 0.02 pixel. Accuracy can be improved by selecting lines of a sufficient signal-to-noise ratio and using a line catalog sorted for blends for the specific spectral resolution of the instrument.

The echelle relation derives from the grating dispersion relation :

with k the grating constant, m the order number, and 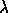the wavelength. The cross-disperser displaces successive orders vertically with respect to one another. For a given position x on the frame, we have :

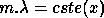(Echelle Relation)

The acurracy of this relation is limited by optical aberrations and optical misalignments, which make it only useful to initialise the calibration process by reducing the number of identifications necessary to determine this one-dimensional relation, expressed as a polynomial of low degree N like:

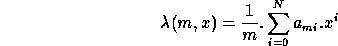
The two major limits of accuracy of the echelle relation are:

• Optical aberrations: the echelle relation does not include the effect of optical aberrations which will displace the lines in the frame and then become a source of unaccuracy when attempting to estimate the echelle relation parameters from a calibration frame. This contributor however will be partially removed by using an appropriate model to fit the echelle relation, like a polynomial of sufficient degree.

• Optical misalignments: Optical misalignments occur between echelle grating and cross-disperser between this latter and detector. The effective misalignment angle can be up to a few degrees (usually less than 3). Over many hundreds pixels, the misalignment error amounts to systematic errors of many pixels, far beyond the seeked accuracy. it is therefore necessary to correct for any rotation of the detector.