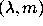 wavelength, spectral order and the space
wavelength, spectral order and the space
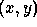 sample x, line y in the raw image. This relation gives the
position of the orders on the raw image, and defines the wavelength
scale of the extracted spectrum. The mapping is performed in two
steps:
sample x, line y in the raw image. This relation gives the
position of the orders on the raw image, and defines the wavelength
scale of the extracted spectrum. The mapping is performed in two
steps:
The first problem in the reduction of echelle spectra is, of course,
the solution of the dispersion relation. That is the mapping between
the space 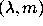 wavelength, spectral order and the space
wavelength, spectral order and the space
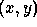 sample x, line y in the raw image. This relation gives the
position of the orders on the raw image, and defines the wavelength
scale of the extracted spectrum. The mapping is performed in two
steps:
sample x, line y in the raw image. This relation gives the
position of the orders on the raw image, and defines the wavelength
scale of the extracted spectrum. The mapping is performed in two
steps:
The second step in the reduction, described in
Section ![]() , is to estimate the image background. The
background depends mainly on the characteristics of the detector, but includes
the additional components of the scattered light in the optics and
spectrograph. This operation corresponds to the step ``Subtract Background''
in fig.
, is to estimate the image background. The
background depends mainly on the characteristics of the detector, but includes
the additional components of the scattered light in the optics and
spectrograph. This operation corresponds to the step ``Subtract Background''
in fig. ![]() .
.
A particular problem in the CCD--detector used by the two
echelle instruments is the appearence of interference fringes produced
within the silicon, which can be especially important in the long
wavelength range of the instrument. By processing the flat-field
(first column of fig. ![]() ), correction
frames are prepared and used for the standard star and the object
reduction. A method to correct for this effect is described in
Section
), correction
frames are prepared and used for the standard star and the object
reduction. A method to correct for this effect is described in
Section ![]() .
.
After the corrections for all these effects, the information in the
spectral orders is extracted using the methods described in
Section ![]() . The extracted flux, used in
conjunction with the dispersion relation, gives the photometric
profiles of the spectral orders. Two instrumental effects are still
present in these profiles: first, due to the blaze effect of the
echelle grating, the efficiency of the spectrograph changes along each
order; second, the efficiency of the whole instrument is not uniform
with wavelength. In Section
. The extracted flux, used in
conjunction with the dispersion relation, gives the photometric
profiles of the spectral orders. Two instrumental effects are still
present in these profiles: first, due to the blaze effect of the
echelle grating, the efficiency of the spectrograph changes along each
order; second, the efficiency of the whole instrument is not uniform
with wavelength. In Section ![]() we describe how
to correct both effects, to normalize the fluxes and, if the input
data includes calibration stars, to convert the fluxes into absolute
units.
we describe how
to correct both effects, to normalize the fluxes and, if the input
data includes calibration stars, to convert the fluxes into absolute
units.
Note a standard star exposure (STD) is a recommended observation strategy which can make easier the order definition in the blue part of the spectrum as well as the correction of individual orders for the variations of grating efficiency (blaze function).
The steps summarised above comprise the STANDARD reduction.
Alternatively, it is possible to correct the variation in sensitivity
along the spectral orders using a suitable model for the blaze
function as described in Section ![]() .
Figure
.
Figure ![]() displays the process scheme
in a typical reduction session; slanted fonts indicate optional
operations. In the rest of this Section the algorithms used in each
step of the reduction are described.
displays the process scheme
in a typical reduction session; slanted fonts indicate optional
operations. In the rest of this Section the algorithms used in each
step of the reduction are described.