


Next: Detecting and Identifying
Up: Long-Slit and 1D
Previous: Flat-Fielding
An accurate two dimensional geometric correction over the entire frame
is an important part of the whole reduction process. It strongly affects
velocity measurements along the slit and is very critical even for
point sources if narrow night sky lines shall be properly subtracted.
If the spectrum contains only a point source the
user may prefer to extract it from the 2D image ( EXTRACT/LONG)
and then proceed with the normal one-dimensional spectral reduction.
On the other hand, if the spatial information along the slit is of no
interest and night sky lines do not have to be corrected for, much time
can be saved by properly averaging the signal along the slit (
EXTRACT/AVERAGE).
The full geometrical correction of long-slit spectra is a
transformation from the raw pixel coordinates 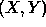 to the sampling space
to the sampling space
 , where
, where  is the wavelength and
s is an angular coordinate in the sky along the slit. Logically,
it often makes sense
to separate the geometrical transformation into two orthogonal components: the
dispersion relation
is the wavelength and
s is an angular coordinate in the sky along the slit. Logically,
it often makes sense
to separate the geometrical transformation into two orthogonal components: the
dispersion relation  , which can be obtained from
an arc spectrum with a fully illuminated slit and the distortion along the
slit
, which can be obtained from
an arc spectrum with a fully illuminated slit and the distortion along the
slit  , which can be derived from the continuum spectra of point
sources. Practically, these two transformations should, whenever possible,
be combined into one before rectifying the data, because this saves one
non-linear rebinning step, each of which necessarily leading to some loss of
information.
, which can be derived from the continuum spectra of point
sources. Practically, these two transformations should, whenever possible,
be combined into one before rectifying the data, because this saves one
non-linear rebinning step, each of which necessarily leading to some loss of
information.
As far as the reduction is concerned, the easiest way to achieve this is
to observe the comparison lamp used for wavelength calibration through a
a pin-hole mask. (Of course, this method can account only for instrumental
distortions, not for differential atmospheric refraction, etc.)
In the presence of strong distortions along the slit, a 2-D modeling must
be attempted and the command RECTIFY/LONG could be considered.
If distortions along the slit can be neglected or
suitably corrected for in a separate step, a 2-D modeling of the dispersion
relation is still a valid approach. However, a separate reduction of detector
row after detector row along the slit, then, often is a superior alternative.
A broad overview of the major options is given in the next subsections;
a detailed comparison and a Cookbook for the usage of the two methods
are provided in Appendix  .
.



Next: Detecting and Identifying
Up: Long-Slit and 1D
Previous: Flat-Fielding
Rein Warmels
Mon Jan 22 15:08:15 MET 1996
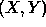 to the sampling space
to the sampling space
 , where
, where  is the wavelength and
s is an angular coordinate in the sky along the slit. Logically,
it often makes sense
to separate the geometrical transformation into two orthogonal components: the
dispersion relation
is the wavelength and
s is an angular coordinate in the sky along the slit. Logically,
it often makes sense
to separate the geometrical transformation into two orthogonal components: the
dispersion relation  , which can be obtained from
an arc spectrum with a fully illuminated slit and the distortion along the
slit
, which can be obtained from
an arc spectrum with a fully illuminated slit and the distortion along the
slit  , which can be derived from the continuum spectra of point
sources. Practically, these two transformations should, whenever possible,
be combined into one before rectifying the data, because this saves one
non-linear rebinning step, each of which necessarily leading to some loss of
information.
, which can be derived from the continuum spectra of point
sources. Practically, these two transformations should, whenever possible,
be combined into one before rectifying the data, because this saves one
non-linear rebinning step, each of which necessarily leading to some loss of
information.