
The dispersion relation is defined by the following equations:
The first of the equations ![]() defines the position of the
spectral orders, m, in the raw image, while the second equation
gives, for each order, the dispersion relation in one dimension. The
mapping between the spaces
defines the position of the
spectral orders, m, in the raw image, while the second equation
gives, for each order, the dispersion relation in one dimension. The
mapping between the spaces 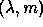 and
and  is separated into
two different equations; the first one will be discussed in this
Section, while the description of the second equation will be
postponed to Section
is separated into
two different equations; the first one will be discussed in this
Section, while the description of the second equation will be
postponed to Section ![]() .
.
The function  is approximated by a polynomial of the form
is approximated by a polynomial of the form
where the coefficients 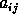 are computed using least squares
techniques on a grid
are computed using least squares
techniques on a grid 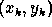 , i.e. sample number and line number
of points located within the spectral orders of the image. These
points in the grid are found automatically by an order--following
algorithm, normally using the FLAT or STD image.
, i.e. sample number and line number
of points located within the spectral orders of the image. These
points in the grid are found automatically by an order--following
algorithm, normally using the FLAT or STD image.
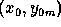 , m being the relative order number.
, m being the relative order number.
 for points on the
right half of the order, and at
for points on the
right half of the order, and at  for points
on the left half of the order,
for points
on the left half of the order,  integer and
integer and 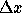 is
the step of the grid.
is
the step of the grid.
This set of points forms the basic grid with the geometric positions of the orders. Typical values of the standard deviation of the residuals of this approximation are about 0.3 to 0.1 pixel.
It is worth mentioning here that the order following algorithm finds the center of the orders by taking the middle point with respect to the edges of the orders. The edges of the orders are detected automatically by thresholding the order profiles, perpendicular to the dispersion direction; the level of the threshold is a function of the signal in the order. The command DEFINE/ECHELLE performs the automatic order detection.
An alternative method is available, based on the Hough transform to perform the order detection and involving a tracing algorithm able to estimate an optimal threshold for each order independently. The order definition is performed as follows:
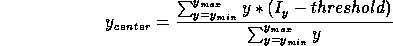
This algorithm is implemented in the command DEFINE/HOUGH. The algorithm can run in a fully automatic mode (no parameters are required apart from the name of the input frame). It is also possible to set the following parameters to enforce a given solution: