


Next: Definition of objects and
Up: Wavelength Calibration
Previous: Offsets between slitlets
Fitting the dispersion curve
Now you have several possibilities to perform your wavelength
calibration. At first there are three different modes to identify
the calibration lines (
 (F)):
(F)):
- Identify:
- You identify at least 2 arc lines in one slitlet
with the command IDENTIFY/MOS. The command CALIBRATE/MOS then
performs a first fit for the CCD row with the identified lines.
- Linear:
- You know the central wavelength and the mean linear
dispersion of your grism. These values are used as first fit of the first
selected CCD row.
You have to correct the value of this central wavelength
if you used the command
OFFSET/MOS to determine the offsets of your slitlets:
- Example:
- Your reference slitlet has an offset of -100 relative to the
center of the CCD in x-direction and you have a mean dispersion of 2Å/pixel
and a central wavelength of 5500Å. This central wavelength will always
lie at the x-position of the respective slitlet, which is in this case
-100 pixels (i.e. -200Å) from the center of the CCD. This
means that you have a wavelength of 5700Å at the center of the CCD
within the reference slitlet. This wavelength should be used as wcenter,
since the program assumes that :xoffset = 0 means that the slitlet is
at the center of the CCD in x-direction.
- Recall:
- Method Linear is performed in the first slitlet.
The dispersion coefficients of the this slitlet is recalled to calibrate the
remaining slitlets. This identification is more stable in this case than for
method Linear and the convergence of the fit is reached faster.
The first fit is used to identify as many lines as possible in the
corresponding CCD row by comparing the fitted line positions to wavelength
catalogue
 .tbl (hear).
For the identified lines a polynomial fit of chosen order is
performed (using Legendre or Chebyshev polynomials - the type being selected
with the keyword
.tbl (hear).
For the identified lines a polynomial fit of chosen order is
performed (using Legendre or Chebyshev polynomials - the type being selected
with the keyword
 (CHEBYSHEV)).
The line identification criterion will identify a computed wavelength
(
(CHEBYSHEV)).
The line identification criterion will identify a computed wavelength
(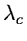 )
with a catalog wavelength (
)
with a catalog wavelength (
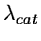 ), if the residual
), if the residual
is small compared to the distances to the next neighbours (in the arc spectrum
as well as in the catalog):
where
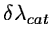 (
(
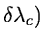 is the distance to the next
neighbour in the catalog (arc spectrum) and
is the distance to the next
neighbour in the catalog (arc spectrum) and 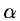 is the tolerance
parameter (0 ...0.5) given by
is the tolerance
parameter (0 ...0.5) given by
 (0.2).
The automatic line identification is repeated with this polynomial
fit in order to identify additional lines
to further improve the dispersion curve.
(0.2).
The automatic line identification is repeated with this polynomial
fit in order to identify additional lines
to further improve the dispersion curve.
Note
For very low dispersion spektroscopy one would expect that a linear
guess will cause line mismatchs at the edge of the detector. One can avoid
this, if more then two lines are identified with method Identify.
After the polynomial fit the residual of each line are checked and the line
is thrown out, if it the residual exceeds the tolerance parameter
 (2) (> 0 - in pixels; < 0 - in units of the wavelength).
One of three fitting methods can be selected by keyword
(2) (> 0 - in pixels; < 0 - in units of the wavelength).
One of three fitting methods can be selected by keyword
 (C):
(C):
- Constant fit in spatial direction:
- the dispersion coeficiants are constant for the whole slitlet. This method is
typically appropriate for small slits.
- Variable fit in spatial direction:
- bad lines are thrown out. Dispersion coeficiants are calculated for any row.
The dispersion relation of the first fitted row is used as estimate for all
following rows. A large number of arc-lines is required for this method.
If there are only a few lines identified at the edge of the detector, small
oscillations at the edge of the detector may occur in spatial direction.
- Two dimensional fit over the slitlet:
- A two-dimensional fit is performed in spatial and dispersion direction over the
slitlet. In spatial direction a ``normal polynom'' is fitted but a polynom
as specified in keyword
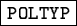 in dispersion direction.
The dispersion coeficiants may smoothly evolve over the slitlet.
This method is the most accurate for most applications, although the resulting
residuals are typically larger than for a variable fit.
in dispersion direction.
The dispersion coeficiants may smoothly evolve over the slitlet.
This method is the most accurate for most applications, although the resulting
residuals are typically larger than for a variable fit.
The iteration is repeated until
a stable solution is obtained (and the minimum number of iterations
 (3) is exceeded) or the maximum number of cycles
(
(3) is exceeded) or the maximum number of cycles
(
 (20)) is reached.
The resulting dispersion coefficients are stored in table
(20)) is reached.
The resulting dispersion coefficients are stored in table
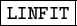 .tbl (coerbr),
together with the r.m.s. error of the fit, the slitlet
and the y-coordinates (world and pixel coordinates).
Also a plot option for the resulting residuals (
.tbl (coerbr),
together with the r.m.s. error of the fit, the slitlet
and the y-coordinates (world and pixel coordinates).
Also a plot option for the resulting residuals (
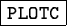 ,
(N))
and various degrees of display (
,
(N))
and various degrees of display (
 ,
(0))
are available.
,
(0))
are available.
After fitting all rows of the respective slitlet with polynomials
of the chosen order
the program performs at last a linear fit to get the central wavelength and the
mean linear dispersion necessary to derive a starting wavelength
for the next slitlet from its known offset (modes Linear/Recall). In the mode
Ident it tries to match the manually identified lines in the next slitlet,
using the known offsets and a maximum allowed shifting tolerance stored
in
 (10).
Rows where no fit could be achieved are stored in the table
(10).
Rows where no fit could be achieved are stored in the table
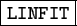 .tbl
with the slit number -1.
.tbl
with the slit number -1.
Any selection of slitlets made in the table
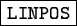 .tbl will be taken
into account, but all selections of the table
.tbl will be taken
into account, but all selections of the table
 .tbl will be ignored.
If you want those to be respected, too, redo the search for the wavelength
calibration lines with the chosen selection in
.tbl will be ignored.
If you want those to be respected, too, redo the search for the wavelength
calibration lines with the chosen selection in
 .tbl.
.tbl.
After the wavelength calibration you may rebin your frame
two-dimensionally to constant wavelength steps with REBIN/MOS.
Point sources are normally wavelength calibrated after extraction (see below).



Next: Definition of objects and
Up: Wavelength Calibration
Previous: Offsets between slitlets
Petra Nass
1999-06-15
![]() (F)):
(F)):
![]() (3) is exceeded) or the maximum number of cycles
(
(3) is exceeded) or the maximum number of cycles
(
![]() (20)) is reached.
The resulting dispersion coefficients are stored in table
(20)) is reached.
The resulting dispersion coefficients are stored in table
![]() .tbl (coerbr),
together with the r.m.s. error of the fit, the slitlet
and the y-coordinates (world and pixel coordinates).
Also a plot option for the resulting residuals (
.tbl (coerbr),
together with the r.m.s. error of the fit, the slitlet
and the y-coordinates (world and pixel coordinates).
Also a plot option for the resulting residuals (
![]() ,
(N))
and various degrees of display (
,
(N))
and various degrees of display (
![]() ,
(0))
are available.
,
(0))
are available.
![]() (10).
Rows where no fit could be achieved are stored in the table
(10).
Rows where no fit could be achieved are stored in the table
![]() .tbl
with the slit number -1.
.tbl
with the slit number -1.
![]() .tbl will be taken
into account, but all selections of the table
.tbl will be taken
into account, but all selections of the table
![]() .tbl will be ignored.
If you want those to be respected, too, redo the search for the wavelength
calibration lines with the chosen selection in
.tbl will be ignored.
If you want those to be respected, too, redo the search for the wavelength
calibration lines with the chosen selection in
![]() .tbl.
.tbl.