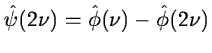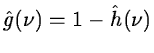


Next: The Reconstruction
Up: Multiresolution with scaling functions
Previous: Multiresolution with scaling functions
We start with the set of scalar products
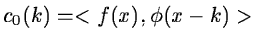 .
If
.
If
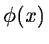 has a cut-off frequency
has a cut-off frequency
 [#starck1<#14704,#starck2<#14705,#starck3<#14706,#starck4<#14707], the data are
correctly sampled. The data at the resolution j=1 are:
[#starck1<#14704,#starck2<#14705,#starck3<#14706,#starck4<#14707], the data are
correctly sampled. The data at the resolution j=1 are:
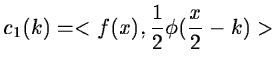 |
|
|
(14.47) |
and we can compute the set c1(k) from c0(k) with a discrete
filter
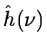 :
:
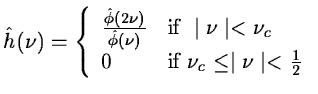 |
|
|
(14.48) |
and
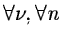 |
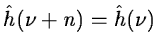 |
|
(14.49) |
where n is an integer.
So:
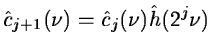 |
|
|
(14.50) |
The cut-off frequency is reduced by a factor 2 at each step, allowing a
reduction of the number of samples by this factor.
The wavelet coefficients at the scale j+1 are:
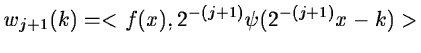 |
|
|
(14.51) |
and they can be computed directly from cj(k) by:
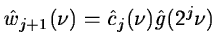 |
|
|
(14.52) |
where g is the following discrete filter:
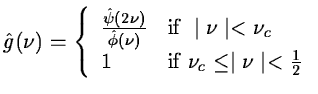 |
|
|
(14.53) |
and
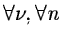 |
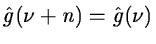 |
|
(14.54) |
The frequency band is also reduced by a factor 2 at each step.
Applying the sampling theorem, we can build a pyramid of
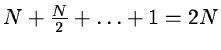 elements.
For an image analysis the number of elements is
elements.
For an image analysis the number of elements is
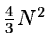 .
The
overdetermination is not very high.
.
The
overdetermination is not very high.
The B-spline functions are compact in this directe space. They
correspond to the autoconvolution of a square function. In
the Fourier space we have:
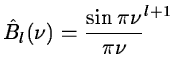 |
|
|
(14.55) |
B3(x) is a set of 4 polynomials of degree 3.
We choose the scaling function 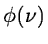 which has a
B3(x) profile in the Fourier space:
which has a
B3(x) profile in the Fourier space:
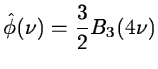 |
|
|
(14.56) |
In the direct space we get:
![$\displaystyle \phi(x)={3\over 8}[{\sin{\pi x\over 4}\over {\pi x\over
4}}]^4$](img712.gif) |
|
|
(14.57) |
This function is quite similar to a Gaussian one and converges
rapidly to 0. For 2-D the scaling function is defined by
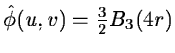 ,
with
,
with
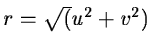 .
It is an isotropic function.
.
It is an isotropic function.
The wavelet transform algorithm with np scales is the following one:
- 1.
- We start with a B3-Spline scaling function and we derive
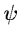 ,
h and
g numerically.
,
h and
g numerically.
- 2.
- We compute the corresponding image FFT. We name T0 the resulting complex array;
- 3.
- We set j to 0. We iterate:
- 4.
- We multiply Tj by
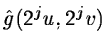 .
We get the complex array
Wj+1. The inverse FFT
gives the wavelet coefficients at the scale 2j;
.
We get the complex array
Wj+1. The inverse FFT
gives the wavelet coefficients at the scale 2j;
- 5.
- We multiply Tj by
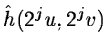 .
We get the array
Tj+1. Its inverse FFT gives the image at the scale 2j+1.
The frequency band is reduced by a factor 2.
.
We get the array
Tj+1. Its inverse FFT gives the image at the scale 2j+1.
The frequency band is reduced by a factor 2.
- 6.
- We increment j
- 7.
- If
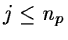 ,
we go back to 4.
,
we go back to 4.
- 8.
- The set
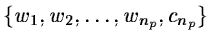 describes the
wavelet transform.
describes the
wavelet transform.
If the wavelet is the difference between two resolutions, we have:
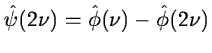 |
|
|
(14.58) |
and:
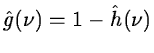 |
|
|
(14.59) |
then the wavelet coefficients
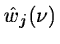 can be computed by
can be computed by
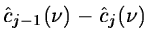 .
.



Next: The Reconstruction
Up: Multiresolution with scaling functions
Previous: Multiresolution with scaling functions
Petra Nass
1999-06-15
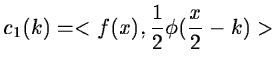
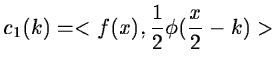
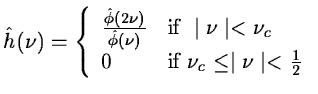
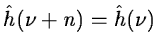
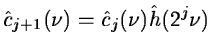
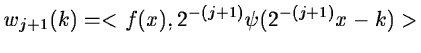
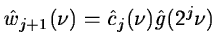
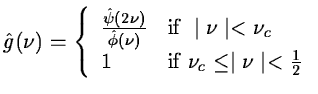
 elements.
For an image analysis the number of elements is
elements.
For an image analysis the number of elements is
![]() .
The
overdetermination is not very high.
.
The
overdetermination is not very high.
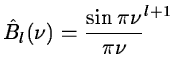
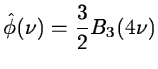
![$\displaystyle \phi(x)={3\over 8}[{\sin{\pi x\over 4}\over {\pi x\over
4}}]^4$](img712.gif)
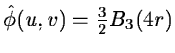 ,
with
,
with
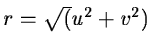 .
It is an isotropic function.
.
It is an isotropic function.
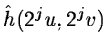 .
We get the array
Tj+1. Its inverse FFT gives the image at the scale 2j+1.
The frequency band is reduced by a factor 2.
.
We get the array
Tj+1. Its inverse FFT gives the image at the scale 2j+1.
The frequency band is reduced by a factor 2.