


Next: Presentation and inspection of
Up: Basic principles of time
Previous: Power of test statistics
Time domain analysis
As noted above, periodic signals are best analysed in the frequency
domain while stochastic signals are usually more profitably analysed
in the time domain. The analysis in the time domain often involves
the comparison of two different signals while in the frequency domain
analyses usually concern only one signal. The expectation value of
the covariance function of uncorrelated signals is zero. The expected
value of the autocorrelation function (E{ACF}, Sect. 12.3.2)
of white noise also is zero everywhere except for 1 at zero lag. The
expected ACF of a stochastic signal of correlation length l vanishes
outside a range  about the lags. The ACF of a deterministic
function does not vanish at infinity. In particular the ACF of a
function with period P has the same value, P. Signals of
intermediate or mixed type with an ACF which has several maxima spaced
evenly by l and a correlation length
about the lags. The ACF of a deterministic
function does not vanish at infinity. In particular the ACF of a
function with period P has the same value, P. Signals of
intermediate or mixed type with an ACF which has several maxima spaced
evenly by l and a correlation length 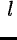 is called a quasiperiodic oscillation. Its power is significantly above the noise
in the
is called a quasiperiodic oscillation. Its power is significantly above the noise
in the
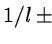 range of frequencies and its correlation length
L is called the coherence length.
range of frequencies and its correlation length
L is called the coherence length.



Next: Presentation and inspection of
Up: Basic principles of time
Previous: Power of test statistics
Petra Nass
1999-06-15
 about the lags. The ACF of a deterministic
function does not vanish at infinity. In particular the ACF of a
function with period P has the same value, P. Signals of
intermediate or mixed type with an ACF which has several maxima spaced
evenly by l and a correlation length
about the lags. The ACF of a deterministic
function does not vanish at infinity. In particular the ACF of a
function with period P has the same value, P. Signals of
intermediate or mixed type with an ACF which has several maxima spaced
evenly by l and a correlation length