


Next: Cluster Analysis
Up: Multivariate Analysis Methods
Previous: Introduction
Among the objectives of Principal Components Analysis are the
following.
- 1.
- dimensionality reduction;
- 2.
- the determining of linear combinations of variables;
- 3.
- feature selection: the choosing of the most useful variables;
- 4.
- visualisation of multidimensional data;
- 5.
- identification of underlying variables;
- 6.
- identification of groups of objects or of
outliers.
The tasks required of the analyst to carry these out are as
follows:
- 1.
- In case of a table of dimensions
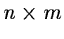 ,
each of the
n rows or objects can be regarded as an m-dimensional vector.
Finding a set of
,
each of the
n rows or objects can be regarded as an m-dimensional vector.
Finding a set of
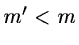 principal axes allows the objects to
be adequately characterised on a smaller number of
(artificial) variables. This is advantageous as a prelude to
further analysis
as the
principal axes allows the objects to
be adequately characterised on a smaller number of
(artificial) variables. This is advantageous as a prelude to
further analysis
as the
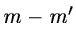 dimensions may often be ignored as
constituting noise; and, secondly, for storage economy
(sufficient information from the initial table is now
represented in a table with
dimensions may often be ignored as
constituting noise; and, secondly, for storage economy
(sufficient information from the initial table is now
represented in a table with
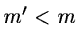 columns).
Reduction of dimensionality is practicable if the first
columns).
Reduction of dimensionality is practicable if the first
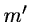 new axes account for approximately 75 % or more of
the variance. There is no set threshold, -- the analyst
must judge. The cumulative percentage of variance
explained by the principal axes is consulted in order
to make this choice.
new axes account for approximately 75 % or more of
the variance. There is no set threshold, -- the analyst
must judge. The cumulative percentage of variance
explained by the principal axes is consulted in order
to make this choice.
- 2.
- If the eigenvalue is zero, the variance of projections on the
associated eigenvector
is zero. Hence the eigenvector is reduced to a point. If this point is
additionally the origin (i.e. the data is centred), then
this allows linear combinations between
the variables to be found. In fact, we can go a
good deal further: by analysing second-order variables,
defined from the given variables, quadratic dependencies
can be straightforwardly sought. This means, for example,
that in analysing three variables, y1, y2, and y3,
we would also input the variables y12, y22, y32,
y1y2, y1y3, and y2y3. If the linear combination
y1 = c1 y22 + c2 y1y2
exists, then we would find
it. Similarly we could feed in the logarithms or other functions
of variables.
- 3.
- In feature selection we want to simplify the task
of characterising each object by a set of attributes.
Linear combinations among attributes must be found; highly
correlated attributes (i.e. closely located attributes in the
new space) allow some attributes to be
removed from consideration; and the proximity of attributes
to the new axes indicate the more relevant and important
attributes.
- 4.
- In order to provide a convenient representation of
multidimensional data, planar plots are necessary. An
important consideration is the adequacy of the planar
representation: the percentage variance explained by the
pair of axes defining the plane must be looked at here.
- 5.
- PCA is often motivated by the search for latent
variables. Often it is relatively easy to label the
highest or second highest components, but it becomes
increasingly difficult as less relevant axes are
examined. The objects with the highest loadings or
projections on the axes (i.e. those which are placed
towards the extremities of the axes) are usually worth
examining: the axis may be characterisable as a spectrum
running from a small number of objects with high positive
loadings to those with high negative loadings.
- 6.
- A visual inspection of a planar plot indicates which
objects are grouped together, thus indicating that they
belong to the same family or result from the same
process. Anomalous objects can also be detected, and
in some cases it might be of interest to redo the
analysis with these excluded because of the perturbation
they introduce.



Next: Cluster Analysis
Up: Multivariate Analysis Methods
Previous: Introduction
Petra Nass
1999-06-15