


Next: Summary of the parameters
Up: Basic Equations
Previous: Optical Depth
Broadening is due both to the natural width of the transition and to the velocity
spread of the absorbing atoms along the line of sight.
- In the ideal case of atoms at rest.
- Let
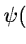 be the normalized distribution of atoms with
velocity between v and
be the normalized distribution of atoms with
velocity between v and
v + dv, then:
![\begin{displaymath}\phi_{\lambda} = \frac {1}{\pi}\ \int_{-\infty}^{+\infty} \ \...
... [\lambda - \lambda_{lk}(1 + \frac {v}{c})]^{2}}
\ \ \psi(v)dv
\end{displaymath}](img353.gif) |
(8.1) |
- In the program the velocity is assumed to be gaussian, thus:
vo = velocity of the cloud relative to the observer.
This full expression (1) is denoted as a ``Maxwell + damping wing''
or ``Voigtian'' profile in the program.
In the case of low column density ( 1)
1)
 can be approximated to:
can be approximated to:
 = NS
= NS

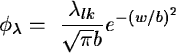 |
(8.2) |
This simplified expression (2) is denoted as a ``Maxwellian'' profile in the
program.
Finally if the line of sight crosses N clouds then, the
resulting optical depth is:
In cases where the source has a (cosmological) velocity.
Let z be the redshift of the source.
An absorption is measured in the spectrum at  =
=
 corresponding to a rest wavelength
corresponding to a rest wavelength
 .
.
This yields for the redshift of the cloud:
The velocity of the cloud relative to the source is:
In practice the program computes the absorption profile in the cloud reference
frame
(vo = 0) and shifts the result into the observer's rest frame
![$\left[ \lambda \rightarrow \frac {\lambda}{1 + Za} \right]$](img371.gif)

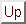


Next: Summary of the parameters
Up: Basic Equations
Previous: Optical Depth
Petra Nass
1999-06-15
![\begin{displaymath}\phi_{\lambda}(v = o) = \frac {1}{\pi}\ \ \frac {\delta_{\lam...
...da)}
{[\delta k (\lambda)]^{2} + (\lambda - \lambda_{lk})^{2}}
\end{displaymath}](img349.gif)
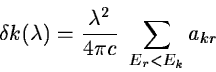
![\begin{displaymath}\phi_{\lambda} = \frac {1}{\pi}\ \int_{-\infty}^{+\infty} \ \...
... [\lambda - \lambda_{lk}(1 + \frac {v}{c})]^{2}}
\ \ \psi(v)dv
\end{displaymath}](img353.gif)
![\begin{displaymath}\phi_{\lambda}(v = o) = \frac {1}{\pi}\ \ \frac {\delta_{\lam...
...da)}
{[\delta k (\lambda)]^{2} + (\lambda - \lambda_{lk})^{2}}
\end{displaymath}](img349.gif)
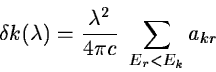
![\begin{displaymath}\phi_{\lambda} = \frac {1}{\pi}\ \int_{-\infty}^{+\infty} \ \...
... [\lambda - \lambda_{lk}(1 + \frac {v}{c})]^{2}}
\ \ \psi(v)dv
\end{displaymath}](img353.gif)
![\begin{displaymath}\psi (v) = \frac {1}{\sqrt \pi} \ \frac {1}{b} \ \exp \ \left[- \ \left(
\frac{v - v_{o}}{b} \right) \right]^{2}
\end{displaymath}](img355.gif)
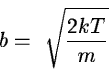
 1)
1)
![]() can be approximated to:
can be approximated to:
![]() = NS
= NS

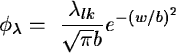
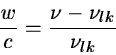
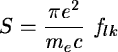
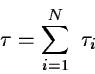
![]() =
=
 corresponding to a rest wavelength
corresponding to a rest wavelength
 .
.
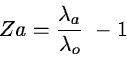
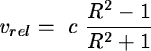
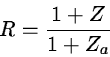
![$\left[ \lambda \rightarrow \frac {\lambda}{1 + Za} \right]$](img371.gif)