



Next: The Quasi-Newton Method.
Up: Outline of the Available
Previous: The Newton-Raphson Method.
From a first guess of the
parameters a(1), a sequence
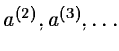 is generated
and is intended to converge to a local minimum of
is generated
and is intended to converge to a local minimum of 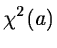 .
At each iteration, one computes
.
At each iteration, one computes
where d(k) is a certain descent direction and
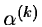 is a real
coefficient which is chosen such that
is a real
coefficient which is chosen such that
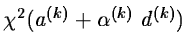 is approximately minimum. The
direction d(k) is ideally the solution of the Newton equation
is approximately minimum. The
direction d(k) is ideally the solution of the Newton equation
H(a(k)) d(k) = -g(a(k))
which can also be rewritten
[J(a(k))T J(a(k)) + B(a(k))] d(k) = -J(a(k)) r(a(k)) .
Neglecting the second derivatives matrix
B(a(k)), we obtain
the ``normal equations'' and the Gauss-Newton direction
J(a(k))T J(a(k)) d(k) = -J(a(k)) r(a(k))
This so-called Gauss-Newton method is intended for problems where
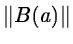 is small. If the Jacobian
J(a) is singular or near singular or if
is small. If the Jacobian
J(a) is singular or near singular or if 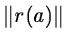 is very large (the
so-called large residuals problem), the Gauss-Newton equation is not a
good approximation of the normal equations and the convergence is not
guaranteed.
is very large (the
so-called large residuals problem), the Gauss-Newton equation is not a
good approximation of the normal equations and the convergence is not
guaranteed.
The algorithm implemented here is a modification
of that Gauss-Newton method, that allows convergence even for
rank deficient Jacobians or for large residuals. The Gauss-Newton
direction is computed in
![$V_1~=~\Im m~[J(a^{(k)})^T~J(a^{(k)})]$](img285.gif) ,
the invariant space corresponding to the non-null eigenvalues.
A correction is taken in V2, the orthogonal of V1,
according to the second derivatives if
the decrease of the objective function at the last
iteration is considered too small.
The Hessian matrix is estimated using finite
differences of the gradient.
,
the invariant space corresponding to the non-null eigenvalues.
A correction is taken in V2, the orthogonal of V1,
according to the second derivatives if
the decrease of the objective function at the last
iteration is considered too small.
The Hessian matrix is estimated using finite
differences of the gradient.
This method requires the availability of the derivatives and as
the number of gradient evaluations is almost p at each iteration, it
is recommended for problems with a small number of parameters,
let us say 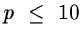




Next: The Quasi-Newton Method.
Up: Outline of the Available
Previous: The Newton-Raphson Method.
Petra Nass
1999-06-09
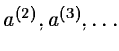 is generated
and is intended to converge to a local minimum of
is generated
and is intended to converge to a local minimum of 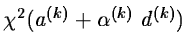 is approximately minimum. The
direction d(k) is ideally the solution of the Newton equation
is approximately minimum. The
direction d(k) is ideally the solution of the Newton equation
![$V_1~=~\Im m~[J(a^{(k)})^T~J(a^{(k)})]$](img285.gif) ,
the invariant space corresponding to the non-null eigenvalues.
A correction is taken in V2, the orthogonal of V1,
according to the second derivatives if
the decrease of the objective function at the last
iteration is considered too small.
The Hessian matrix is estimated using finite
differences of the gradient.
,
the invariant space corresponding to the non-null eigenvalues.
A correction is taken in V2, the orthogonal of V1,
according to the second derivatives if
the decrease of the objective function at the last
iteration is considered too small.
The Hessian matrix is estimated using finite
differences of the gradient.
![]()