
We will examine here the computation of a convolution by using the continuous wavelet transform in order to get a framework for linear smoothings. Let us consider the convolution product of two functions:

We introduce two real wavelets functions  and
and 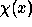 such that:
such that:

is defined.
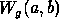 denotes the wavelet transform of g with the wavelet
function
denotes the wavelet transform of g with the wavelet
function 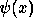 :
:
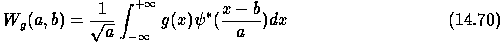
We restore 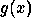 with the wavelet function
with the wavelet function 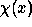 :
:

The convolution product can be written as:
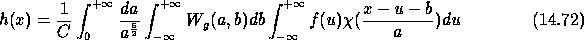
Let us denote  . The wavelet transform
. The wavelet transform  of
of 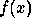 with
the wavelet
with
the wavelet 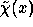 is:
is:

That leads to:
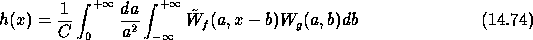
Then we get the final result:
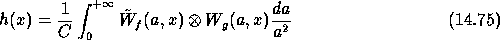
In order to compute a convolution with the continuous wavelet transform:
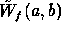 of the function
of the function 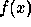 with the
wavelet function
with the
wavelet function 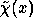 ;
;
 of the function
of the function 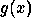 with the
wavelet function
with the
wavelet function  ;
;
The wavelet transform permits us to perform any linear filtering.
Its efficiency depends on the number of terms in the wavelet
transform associated with  for a given signal
for a given signal 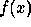 . If we
have a filter where the number of significant coefficients is
small for each scale, the complexity of the algorithm is
proportional to N. For a classical convolution, the complexity
is also proportional to N, but the number of operations is also
proportional to the length of the convolution mask. The main
advantage of the present technique lies in the possibility of having a
filter with long scale terms without computing the convolution on
a large window. If we achieve the convolution with the FFT
algorithm, the complexity is of order
. If we
have a filter where the number of significant coefficients is
small for each scale, the complexity of the algorithm is
proportional to N. For a classical convolution, the complexity
is also proportional to N, but the number of operations is also
proportional to the length of the convolution mask. The main
advantage of the present technique lies in the possibility of having a
filter with long scale terms without computing the convolution on
a large window. If we achieve the convolution with the FFT
algorithm, the complexity is of order  . The computing time is
longer than the one obtained with the wavelet transform if we
concentrate the energy on very few coefficients.
. The computing time is
longer than the one obtained with the wavelet transform if we
concentrate the energy on very few coefficients.