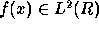The Morlet-Grossmann definition of the continuous wavelet
transform [17] for a 1D signal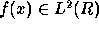 
is:
where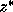 
denotes the complex conjugate of z, 
is the
analyzing wavelet, a (>0) is the scale parameter and b is
the position parameter. The transform is characterized by the
following three properties:
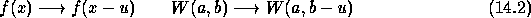
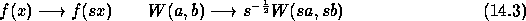
In Fourier space, we have:
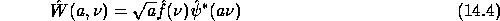
When the scale a varies, the filter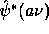 
is only reduced or
dilated while keeping the same pattern.
Now consider a functio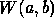n 
which is the wavelet transform of a
given function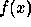 
. It has been shown
[,] that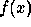 
can be restored using the
formula:
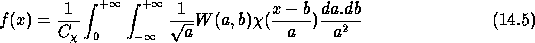
where:
Generally 
, but other choices can enhance certain features
for some applications.
The reconstruction is only available if 
is defined (admissibility
condition). In the case of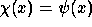 
, this condition implies
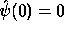, i.e. the mean of the wavelet function is 0.
