
The wavelength calibration involves a physical equation, the echelle relation and regression analysis to achieve estimates of the dispersion relation. Provided that the echelle dispersion is performed with a grating, any echelle spectrum can be calibrated usually with four lines used as pre-identifications and a catalog of laboratory wavelengths associated to the calibration lamp. The achieved accuracy is usually in the range 0.2 - 0.02 pixel. Accuracy can be improved by selecting lines of a sufficient signal-to-noise ratio and using a line catalog sorted for blends for the specific spectral resolution of the instrument.
The echelle relation derives from the grating dispersion relation :

with k the grating constant, m the order number, and 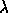 the wavelength.
The cross-disperser displaces successive orders vertically with respect
to one another. For a given position x on the frame, we have :
the wavelength.
The cross-disperser displaces successive orders vertically with respect
to one another. For a given position x on the frame, we have :
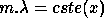 (Echelle Relation)
(Echelle Relation)
The acurracy of this relation is limited by optical aberrations and optical misalignments, which make it only useful to initialise the calibration process by reducing the number of identifications necessary to determine this one-dimensional relation, expressed as a polynomial of low degree N like:
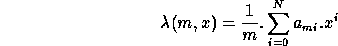
The two major limits of accuracy of the echelle relation are: